Fundamentals of Fluid Pumping

Pumps are vital equipment in every refinery and petrochemical plant. They are the mostly used rotary equipment in oil, gas and energy industry. Therefore, it is important to understand the principles and hydraulics of pumps. They provide the required pressure for the low pressure liquid. Pumps use either electrical power (electromotor driven) or an external flow of steam (turbine driven) as their source of energy. They converts this energy to fluid’s pressure.

In this article, which is the first part of pump series, we will review Fundamentals of Fluid Pumping. First, we will study the important concepts of energy and Bernoulli’s equations. Then, we will review the system curve in a pumping circuit. Finally, we will focus our attentions into cavitation phenomenon and NPSH terms and theories for centrifugal pumps.

Main Contents:

• Energy balance
• Bernoulli’s principle
• Hydraulic system of fluid transfer
• Cavitation
• NPSH

The total energy of a fluid in motion is the sum of four individual energies. Internal, potential, pressure and kinetic energies. For a convenient analogy, these energies are expressed in unit mass of fluids:

• Internal energy is the energy of atoms and molecules resulting from their motion and configuration. For Incompressible fluids like liquids, internal energy is a function of temperature. It is increases with a rise in temperature. The internal energy per unit of mass is denoted by “U”.
• Potential energy is the energy of the fluid relative to its elevation from an arbitrarily level in the earth’s gravity field (g). Literally, it is the work required to lift up a unit mass of fluid to a particular height (z) from an arbitrarily chosen place. Potential energy is express by “zg”.
• Pressure energy is equal to the work required to enter a fluid into the system in a constant volume. Therefore, this energy can be defined by PV/m. Where P is pressure and V is the volume of mass By substituting fluid density (\rho ), the pressure energy becomes equal to “ P/\rho ”.
• Kinetic energy is the energy of liquid due to its motion. It’s equal to u²/2, where u is the velocity of the fluid.

Thus, total energy E is defined by the following equation: E=U+zg+\frac{P}{\rho }+\frac{u^{2}}{2} For a steady state process, where there is no accumulation in the system, the change in total energy of a fluid is equal to the sum of heat (Q) and work (W) transferred to the fluid. According to thermodynamic law, the energy balance is: E_{2}-E_{1}= Q+W_{p}+W_{f} Where W_p is the work transferred into the fluid by means of a pump and W_f is the work done by the fluid to overcome viscous frictional forces. If no heat transfer takes place and assume the temperature remains constant, the energy balance may be written as:

\left ( z_{1}g+\frac{P_{1}}{\rho }+\frac{u_{1}^{\: 2}}{2} \right )+W_{p} = \: \: \: \: \: \: \: \: \: \: \: \: \: \: \left ( z_{2}g+\frac{P_{2}}{\rho }+\frac{u_{2}^{\: 2}}{2} \right )+W_{f}

In engineering calculations, it is more convenient to deal with this equation in terms of length dimension. Therefore, dividing throughout by g, the final energy equation becomes:

\left ( z_{1}+\frac{P_{1}}{\rho g}+\frac{u_{1}^{\: 2}}{2g} \right )+h_{p} = \: \: \: \: \: \: \: \: \: \: \: \: \: \: \left ( z_{2}+\frac{P_{2}}{\rho g}+\frac{u_{2}^{\: 2}}{2g} \right )+h_{f}

These terms are known as potential, pressure and velocity heads. h_p is the head produced by the pump and h_f is the head loss due to friction. They are all have the unit of length.

In fluid mechanics, head is defined as fluid pressure divided by fluid’s density and earth’s gravitational acceleration: H=\frac{P}{\rho g} Head is a type of pressure. It has a unit of length. In fact, engineers prefer using head quantity to pressure for the ease of calculations and comparison of different systems.

Bernoulli’s equation is the simple form of energy balance in incompressible fluids. It is expressed in terms of heads usually without pump and frictional heads: z_{1}+\frac{P_{1}}{\rho g}+\frac{u_{1}^{\: 2}}{2g} = \ z_{2}+\frac{P_{2}}{\rho g}+\frac{u_{2}^{\: 2}}{2g} Bernoulli’s principle implies that the total energy of a fluid always remains constant if there is no friction loss and pump’s works. The total energy which is the sum of potential, pressure and kinetic energies is known as energy grade line. Since these forms of energy are interchangeable, energy is converted from one form to another. This equation is a handy tool for engineers to calculate potential, pressure and kinetic head of a stream at different positions.

Assumption to derive Bernoulli’s equation:

• The fluid is incompressible.
• Internal energy of the fluid remains constant. This is not the case where frictional dissipations causes a rise in fluid’s temperature. In such a case, the internal energy increases.
• The flow is at steady state condition
• It is only valid between two points along the same streamline. Fluids flowing along different streamlines have different total energy.

Bernoulli’s equation is very accurate for turbulent flow of liquid across a pipe or duct. However, for a Newtonian laminar flow, it shall be used by caution. The reason is the kinetic energy of an element flowing at the center of the pipe in laminar flow is different from that of an element flowing near the wall due to the lower velocity near the pipe. Therefore, the kinetic head shall be multiplied by a dimensionless correction factor of “2”, which account for the velocity distribution across the pipe or duct.

According to figure 1, water is flowing through a pipe with internal diameter of 8” and a pressure of 4 bara at point A. Then it enters an inclined pipe with a diameter of 6”. Calculate the pressure at point B. The flowrate is 200,000 kg/hr and the density of water is 1000 m³/kg. Assume friction loss is negligible.

Figure 1

Solution:

Using Bernoulli’s equation and applying the law of continuity for point A & B: 0+\frac{4\times 10^{5}}{1000\times 9.8}+\frac{u_{A}^{\: 2}}{2\times 9.8} = \: \: \: \: \: \: \: \: \: \: \: \: \: \: 10+\frac{P_{B}}{1000\times 9.8}+\frac{u_{B}^{\: 2}}{2\times 9.8} \dot{m}_{A}=\dot{m}_{B}\; \rightarrow \; \rho S_{A}u_{A}=\rho S_{B}u_{B} Where \dot{m} is mass flow rate and S is pipe’s cross sectional area. From equation of continuity u_A=1.8 m/s and u_B=3.1 m/s. By substituting u_A and u_B into Bernoulli’s equation, P_B is calculated as 3 bara. Note that in this example the kinetic term have a minor effect on the final answer due to the low velocity.

Consider a system consisting of two tanks with specific liquid level relative to the reference level (ground). A pump is used to pump the liquid from tank 1 to 2. These tanks are under the static pressure of P₁ and P₂. The overall pipeline has an overall velocity friction factor of K due to the pipes and the fittings pressure loss. Figure 2 illustrates this system.

Figure 2

By applying the Bernoulli’s principle for point 1 and 2 and adding the terms related to pump and friction loss heads, the following equations is obtained for the above system:

\left ( z_{1}+\frac{P_{1}}{\rho g}+\frac{u_{1}^{\: 2}}{2g} \right )+h_{p}-h_{f} = \: \: \: \: \: \:  \: \: \: \: \: \: \: \: \: \: \: \:  \left ( z_{2}+\frac{P_{2}}{\rho g}+\frac{u_{2}^{\: 2}}{2g} \right ) h_{f}=K\frac{u_{p}^{\: 2}}{2g} Where u_p is the fluid velocity inside the pipes. Since the velocity of fluids in the tanks is negligible, the kinetic energy can be ignored. Solving the equation for pump’s head: h_{p}=\left ( z_{2}-z_{1} \right )+\left ( \frac{P_{2}-P_{1}}{\rho g} \right )+K\frac{u_{p}^{\: 2}}{2g} In the above equation, all of the parameters are pre-defined and constant except u_p . In addition, since u_p is directly proportional to volumetric flowrate Q, we can simply replace this equation with the following relation:

h_{p}=A+BQ^{2}

Where A and B are equivalent constant coefficients. This relation illustrates that pump’s head is a quadratic function of volumetric flowrate.

Figure 3

Figure 3 is a famous curve, known as system hydraulic curve. As shown in the figure, the required pump’s head becomes larger as flowrate increases. This is because of an increase in piping pressure loss due to the higher fluid’s speed. Engineers often utilize this curve as an important tool for selecting a proper pump. In order to estimate the operating point of a centrifugal pump engineers draw the system curve and pump’s performance curve in a same plot. The point at which these two curves intersect is the estimated operating point of the system.

Cavitation is a negative physical phenomenon occurs when fluid’s static pressure becomes less than liquid vapor pressure (P < P*). In this case, the liquid partially vaporizes forming localized bubbles. When fluid’s pressure exceeds liquid vapor pressure again, these bubbles collapse releasing a strong destructive pressure wave. We often observe this phenomenon behind a boat’s propeller under the water when the boat starts moving. In the following video clip, we can see the formation and the collapse of cavitation bubbles with a diameter of approximately 9 mm in slow motion. This process takes about 4 milliseconds in real time.

In oil, gas and petrochemical applications, cavitation mostly occurs at pump’s suction side especially at the eye of impeller. Where the liquid static pressure becomes less than liquid vapor pressure. As the vapor bubbles are carried into higher pressure region of the pump, they collapse resulting in noise and vibration. The noise caused by cavitation sounds as if sand particles passing through the pump.

Cavitation causes the following problems to the pump:

• Reduce efficiency
• Pulsation in discharge liquid flowrate
• Impeller damage
• Internal parts surface erosion
• High vibration and noise

Impeller cavitation corrosion (courtesy of KSB Group)

Suction side static pressure and liquid temperature are two important parameters affecting the rate of cavitation. The less the suction pressure the more the rete of cavitation. In addition, the more the temperature the more the liquid vapor pressure which, again, increase the rate of cavitation.

Occurrence of cavitation in centrifugal pumps have some particular signs. It is very important to identify these signs and take action promptly prior to any serious damage to pump. Some of the main symptoms of cavitation in centrifugal pumps are:

• Pumps stars making lots of noise
• Vibration increases dramatically
• Discharge pressure and flowrate decreases
• Bearings fail so quickly
• Failure of pump’s internal parts

Net positive suction head, known as NPSH, is one of the most important terms in pump’s design. It is the difference between the suction head and the liquid vapor pressure head at pump’s inlet nozzle. As its name suggests, NPSH is reported in unit of length.

For a liquid at suction of a pump if there is a head reduction equal to NPSH value, cavitation occurs causing the formation of bubbles. In other words, the static pressure of the suction liquid shall be always greater than its vapor pressure. NPSH main usage is to prevent cavitation at the inlet of the pump. Pump’s manufacturers design their pump based on the available NPSH reported by the purchaser in order to guarantee no cavitation occurs at normal pump operation. There are two kinds of NPSH: NPSHa and NPSHr.

NPSHa, in which “a” stands for available, is one of the system characteristics. It is calculated by pump’s purchaser based on the suction side conditions of the pump. NPSHa is the difference between suction head and liquid vapor pressure. Therefore, if calculated NPSHa is too small (e.g. less than one meter), there is a high risk that cavitation occurs. NPSHa can be calculated as the total static head at upstream equipment minus suction-side pressure loss head minus liquid vapor pressure head: NPSHa=\frac{1}{\rho g}\left ( P_{ue}-\Delta P_{s}-P^{ *} \right ) Where P_ue is the pressure at upstream equipment and \Delta P_{s} is the pressure loss of suction side.

Calculate NPSH available for a pump which is used downstream of an atmospheric tank with a liquid level of 10 meters relative to pimp’s centerline. Suction side friction loss due to pipes and fittings is 0.1 bar and liquid vapor pressure at operating temperature is 0.5 bara. Liquid density is 1000 kg/m³.

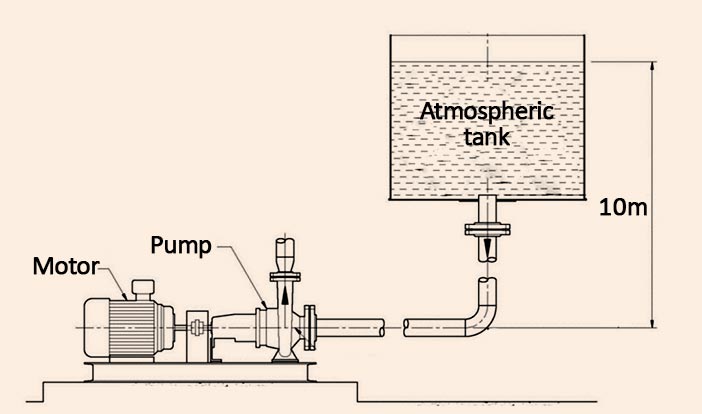
Solution: (SI units)  NPSHa=z-\frac{1}{\rho g}\left ( \Delta P_{s}+P^{ *} \right ) NPSHa=  10-\frac{1}{1000\times 9.8}\left ( 0.1\times 10^{5}+0.5\times 10^{5}\right ) =3.9 m 

NPSHr, also called NPSH3, is related to pump’s characteristic. It is dictated by pump’s geometry. “r” letter, at the end of NPSHr, stands for required. Literally, NPSHr indicates the minimum NPSH required at the suction of the pump in order for the pump to operate without cavitation.

In order to guarantee a smooth operation without cavitation, NPSHa shall be always greater than NPSHr by a safe margin. NPSHr< NPSHa The above inequality shall be satisfied for the whole range of flowrate of centrifugal pump from minimum flow to maximum allowable flow. The more the difference between NPSHa and NPSHr the less probable the cavitation to occur. It’s recommended that:

• If NPSHa – NPSHr < 2 ft : Do not use the pump
• If NPSHa – NPSHr < 3 ft : NPSH test is necessary

There is no exact theoretical equation to calculate NPSHr. Thus, this value has to be determined experimentally or by numerical analysis of fluid flows. Pump’s manufacturers often obtain NPSHr of their pumps by means of computational fluid dynamics (CFD) software. However, this value has to be tested for most pumps individually after fabrication. There are some methods presented in “ISO 9906 standard” as well as “API standard 610” to determine NPSHr for centrifugal pumps. One of the most popular methods is as follows:

“While the pump is in operation, at constant flowrate, decrease the NPSHa gradually by closing a throttling valve installed on the suction line of the pump. As soon as there is a sudden reduction of 3% in pump’s head, cavitation occurs. In this point NPSHa becomes equal to NPSHr. By calculating the available NPSH at this point, NPSHr can be obtained according to the following equation:” NPSHr=\frac{1}{\rho g}\left ( P_{in}-P^{*} \right )+\frac{u_{in}^{\: 2}}{2g} Where P_in is the absolute pressure at pump’s inlet at 3% head drop and u_in is the liquid velocity at pump’s inlet.

Typical methods to decrease NPSHa for an NPSH test:

• Use a throttling valve on suction line
• Decrease the liquid level in upstream suction tank
• Decrease the pressure in suction tank by means of a vacuum pump
• Different combinations of the above methods

As a result, NPSHr can be determined by performing an NPSH test. When the pump’s discharge head drops by 3%, NPSHr becomes equal to available NPSH at the suction of the pump. This is the point where cavitation begins. API refers to NPSHr as “NPSH3” because of the 3% drop in head.

Hydrocarbons liquids in oil, gas and petrochemical plants, have higher vapor pressure than water. However, experimental data shows that they have lower NPSHr comparing to water. some reasons for this strange fact are:

• Collapsing of hydrocarbon’s bubbles releases less energy comparing to water.
• Hydrocarbons have lower vapor volume. Therefore, if they vaporize, they occupy less area.

As a result, since NPSH test is always carried out by liquid water, there are some hydrocarbon correction factors which is used to compensate for hydrocarbons properties.

There are two practical ways to stop cavitation from happening in centrifugal pumps. Increase NPSHa and decrease NPSHr. Since NPSHa is a system parameter, there are limitations to increase it. On the contrary, NPSHr is related to pump’s specifications and can be altered by a more efficient pump’s design.

Increasing NPSHa

• Increase suction tank’s pressure
• Increase suction tank’s liquid level
• Cool down the liquid in order to decrease its vapor pressure
• Install the pump at the lower elevation
• Install a suction line with greater pipe’s diameter and minimum fittings

Decreasing NPSHr

• Use an impeller with larger eye
• Decrease pump’s rotational speed
• Install a booster pump at suction
• Use double suction impeller
• Install an inducer before impeller
• Use smaller pumps in parallel arrangement

Hydraulic principles and concepts of liquid pumping plays an important role in designing/selecting a proper pump for engineers. Criteria used in oil, gas and petrochemical industry are stricter than others are. Therefore, a better understanding of pumping system’s fundamentals is necessary. In this article, we reviewed the energy laws of fluids system and explained the important concepts of Bernoulli’s principle. Then we talked about the principle of pumping system hydraulic. Finally, we reviewed the complete definitions and theories of cavitation and NPSH according to practical industrial applications.